miércoles, 13 de febrero de 2013
martes, 12 de febrero de 2013
“1.6. CUANTILES”
Los
cuantiles son aquellos valores de la variable, que ordenados de menor a mayor,
dividen a la distribución en partes, de tal manera que cada una de ellas
contiene el mismo número de frecuencias.
Constituyen
una generalización del concepto de mediana. Así como la mediana divide a la
serie estudiada en dos partes con el mismo número de elementos cada una, si la
división se hace en cuatro partes, o en diez partes, o en cien partes, llegamos
al concepto de cuantil.
Hay, principalmente, tres
cuantiles importantes: cuartiles, deciles y percentiles:
Cuartiles
Son
tres valores con las siguientes características:
Q1: Primer
cuartil, que es el valor de la variable por debajo del cual queda 1/4 de los
elementos de la serie estudiada.
Q3: Tercer
cuartil, que es el valor de la variable por debajo del cual quedan los 3/4 de
los elementos que constituyen la serie.
Evidentemente el segundo
cuartil coincide con la mediana. Como puede comprobarse, no tendría ninguna utilidad
definir el cuarto cuartil. El cálculo de los cuartiles se realiza por el mismo
procedimiento que el cálculo de la mediana, pues hay únicamente una diferencia
cuantitativa entre ambas medidas, pero tienen significados paralelos.
Percentiles
Hay
99 percentiles que se denotan: P1, P2, P3,.......,P98,
P99. Así P90, por ejemplo, deja por debajo de él el 90%
de los elementos.
Ejercicio: De la siguiente
serie hallar el primero y el tercer cuartil, el segundo y el séptimo decil y
los percentiles 8 y 73.
Resp: Q1 = 34,82;
Q3 = 47,36; D2 = 32,85; D7 = 45,83; P8
= 26,94; P73 = 46,75.
Obsérvese que entre los 6
cuantiles calculados, aparecen valores muy parecidos. En particular se dan las
siguientes coincidencias:
Ø El segundo cuartil
equivale a la mediana.
Ø El quinto decil y el
quincuagésimo percentil se corresponden también con la mediana.
Ø Los percentiles P25
y P75 se corresponden con el primer y tercer cuartil,
respectivamente.
Deciles
Es
la segunda clase de cuantiles. Si se divide toda la serie en diez partes
iguales tendremos los deciles.
D1, el decil 1,
deja el 10% de los valores de la serie por debajo de él.
Análogamente ocurre con los
deciles D2, D3,.......D9. El decil 8, por
ejemplo, deja el 80% de la masa de datos investigada por debajo de él.
Las fórmulas para
calcularlos son también análogas a las de la mediana.
“1.7 GRÁFICOS”
Las representaciones gráficas deben conseguir que un simple
análisis visual ofrezca la mayor información posible.
Según el tipo de carácter que estemos estudiando,
usuraremos un grafico u otro.
Según
sea la variable, los gráficos más utilizados son:
-
Diagramas de barra.
-
Diagramas de sectores
-
Histogramas
Diagrama de barras
Es
un tipo de gráfico estadístico que se utiliza para variables cualitativas y
discretas.
En el eje X se sitúan:
§ Las
modalidades de la variable cualitativa.
§ Los
valores de la variable cualitativa discreta.
Y sobre ellos se levantan
barras cuya altura sea proporcional a sus frecuencias.
Histogramas
Se
utilizan con variables continuas, o agrupadas en intervalos, representando en
el eje X los intervalos de clase y levantando rectángulos de base la longitud
de los distintos intervalos y de altura tal que el área sea proporcional a las
frecuencias representativas.
El polígono de frecuencias se obtiene uniendo los puntos medios de las bases
superiores de los rectángulos.
Los histogramas permiten compara datos de una forma rápida (basta mirar la
gráfica).
Pirámides de población
Cuando se realizan representaciones correspondientes a edades de población,
cambiamos el eje Y por el eje X para obtener las llamadas pirámides de
población, que no son más que 2 histogramas a izquierda y derecha, para
hombres y mujeres.
Diagramas de sectores
Es
un gráfico empleado fundamental mente para variables cualitativas. Las
modalidades se representan en un círculo dividido en sectores.
La
amplitud de cada sector, en grados, se obtiene multiplicando la frecuencia
relativa de cada modalidad o valor por 360°
“1.8 CAJAS Y ALAMBRES”
Un
diagrama de caja es un gráfico, basado en cuartiles, mediante el cual se
visualiza un conjunto de datos. Está compuesto por un rectángulo, la
"caja", y dos brazos, los "bigotes".
Es
un gráfico que suministra información sobre los valores mínimo y máximo, los
cuartiles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y la
simetría de la distribución. Primero es necesario encontrar la mediana para
luego encontrar los 2 cuartiles restantes
Cómo
expresarlo gráficamente:
+-----+-+
*
o |-------| | |---|
+-----+-+
+---+---+---+---+---+---+---+---+---+---+---+---+
0 5 10 12
Ordenar los datos y obtener el
valor mínimo, el máximo, los cuartiles Q1, Q2 y Q3 y el Rango Inter Cuartilico
(RIC)
En el
ejemplo:
·
Valor 7: es el Q1 (25% de los
datos)
·
Valor 8.5: es el Q2 o mediana
(el 50% de los datos)
·
Valor 9: es el Q3 (75% de los
datos)
·
Rango Inter Cuartilico RIC
(Q3-Q1)=2
Para dibujar los bigotes, las
líneas que se extienden desde la caja, hay que calcular los límites superiores
e inferiores, Li y Ls, que identifiquen a los valores atípicos.
Para ello se calcula cuándo se consideran atípicos los valores. Son
aquellos inferiores a Q1-1.5*RIC o superiores a Q3+1.5*RIC.
En el ejemplo:
·
inferior: 7-1.5*2=4
·
superior: 9+1.5*2=12
Ahora se buscan los últimos valores que NO son
atípicos, que serán los extremos de los bigotes.
·
En el ejemplo: 5 y 10
Marcar como atípicos todos los
datos que están fuera del intervalo (Li, Ls).
·
En el ejemplo: 0.5 y 3.5
Además, se pueden considerar
valores extremadamente atípicos aquellos que exceden Q1-3*RIC o Q3+3*RIC. De
modo que, en el ejemplo:
·
inferior: 7-3*2=1
·
superior: 9+3*2=15
“1.9. DIAGRAMA DE PARETO”
El diagrama de Pareto, también llamado curva 80-20 o Distribución C-A-B, es una gráfica para organizar datos de forma
que estos queden en orden descendente, de izquierda a derecha y separados por
barras. Permite, pues, asignar un orden de prioridades.
El diagrama permite mostrar
gráficamente el principio de Pareto (pocos
vitales, muchos triviales), es decir, que hay muchos problemas sin importancia
frente a unos pocos graves. Mediante la gráfica colocamos los "pocos
vitales" a la izquierda y los "muchos triviales" a la derecha.
El diagrama facilita el estudio de las
fallas en las industrias o empresas comerciales, así como fenómenos sociales o
naturales psicosomáticos, como se puede ver en el ejemplo de la gráfica al
principio del artículo.
Hay que tener en cuenta que tanto la
distribución de los efectos como sus posibles causas no es un proceso lineal
sino que el 20% de las causas totales hace que sean originados el 80% de los
efectos.
El principal uso que tiene el elaborar
este tipo de diagrama es para poder establecer un orden de prioridades en la toma de decisiones dentro de una organización. Evaluar
todas las fallas, saber si se pueden resolver o mejor evitarlas.
Se recomienda el uso del diagrama de Pareto:
-
Para
identificar oportunidades para mejorar
- Para identificar un producto o servicio para el
análisis de mejora de la calidad.
- Cuando existe la necesidad de
llamar la atención a los problemas o causas de una forma sistemática.
- Para analizar las diferentes
agrupaciones de datos.
- Al buscar las causas principales
de los problemas y establecer la prioridad de las soluciones.
- Para evaluar los resultados de
los campos efectuados a un proceso comparando sucesivos diagramas.
- Obtenidos en momentos diferentes,
(antes y después).
- Cuando los datos puedan clasificarse
en categorías.
- Cuando el rango de cada categoría
es importante.
-
Para
comunicar fácilmente a otros miembros de la organización las conclusiones sobre
causas, efectos y costes de los errores.
Los propósitos generales del diagrama de Pareto:
-
Analizar las
causas.
- Estudiar los resultados.
-
Planear
una mejora continua.
La Gráfica de Pareto es una
herramienta sencilla pero poderosa al permitir identificar visualmente en una
sola revisión las minorías de características vitales a las que es importante prestar
atención y de esta manera utilizar todos los recursos necesarios para llevar a
cabo una acción de mejora sin malgastar esfuerzos ya que con el análisis
descartamos las mayorías triviales.
Algunos ejemplos de tales minorías vitales serían:
-
La minoría
de clientes que representen la mayoría de las ventas.
- La minoría de productos,
procesos, o características de la calidad causantes del grueso de desperdicio o
de los costos de re trabajos.
- La minoría de rechazos que
representa la mayoría de quejas de los clientes.
- La minoría de vendedores que está
vinculada a la mayoría de partes rechazadas.
- La minoría de problemas causantes
del grueso del retraso de un proceso.
- La minoría de productos que
representan la mayoría de las ganancias obtenidas.
-
La
minoría de elementos que representan la mayor parte del costo de un inventario etc.
“1.10. USO DE SOFTWARE”
El uso de ordenadores
y calculadoras facilita el que los alumnos comprendan mejor temas complejos de
matemáticas. Es evidente que en muchos casos la tecnología agiliza y supera, la
capacidad de cálculo de la mente humana, con ayuda de la tecnología, los
alumnos tienen más tiempo para concentrarse en enriquecer su aprendizaje
matemático.
Las nuevas
tecnologías han venido a cambiar por completo el panorama tradicional de cómo
se hacían, se veían y se enseñaban las matemáticas. Introducirse en este nuevo
panorama implica realizar profundos cambios en nuestros programas educativos.
Es muy amplia la variedad de aplicaciones informáticas disponibles para estadística y probabilidad:
Es muy amplia la variedad de aplicaciones informáticas disponibles para estadística y probabilidad:
Excel o Calc
Javascript
Applet de Java, Geogebra
Proyecto Descartes
Software Libre
Otros Software
Ejercicio: Estadística Bidimensional
Se observaron las edades
de cinco niños y sus pesos respectivos y se consiguieron los resultados
siguientes:
Edad
|
2
|
4,5
|
6
|
7,2
|
8
|
Peso
|
15
|
19
|
25
|
33
|
34
|
a) Hallar las medias y desviaciones marginales.
Introducimos los datos en las
celdas: en la columna A la edad y la B el peso.
A continuación podemos
hacer clic con el ratón en "Función fx", del menú "Insertar”,
apareciendo la ventana de diálogo "Pegar función", donde podemos
seleccionar las funciones estadísticas y las funciones que queramos calcular; o
bien directamente, si conocemos la sintaxis de las funciones estadísticas,
editamos dichas funciones. Situamos el puntero en la columna D y vamos
tecleando cada una de las funciones estadísticas en la barra de fórmulas,
situando el puntero cada vez en una celda distinta para ir conservando los
datos. De esta forma, las medias y desviaciones marginales
se calculan:
=PROMEDIO (A2:A6), obtenemos la media de
la edad.
=PROMEDIO (B2:B6), obtenemos la media del
peso.
=DESVESTP (A2:A6), obtenemos la desviación
típica de la edad.
=DESVESTP (B2:B6), obtenemos la desviación
típica del peso.
Para calcular el coeficiente de
correlación, tecleamos en la barra de fórmulas
=COEF.DE.CORREL (A1:A6, B2:B6), una vez situados en la celda que queramos.
=COEF.DE.CORREL (A1:A6, B2:B6), una vez situados en la celda que queramos.
=PENDIENTE (B2:B6, A2:A6) nos informa
sobre la pendiente de la recta de regresión del
peso sobre la edad, en la celda donde queramos.
Por tanto, usando
nuestros conocimientos estadísticos, tenemos que la recta de regresión es:
y - 25,2 = 3,4049(x - 5,54).
También podemos calcular
la recta de regresión haciendo clic en "Función fx",
del menú "Insertar" y seleccionando la función ESTIMACION.LINEAL de
las funciones estadísticas.
En la pantalla aparecen
los valores de "a" y b", siendo y = bx + a, recta de
regresión de Y sobre X. Por tanto la recta de regresión es: y = 3,4049x +
6,33678.
Excel incorpora dos
funciones que nos permiten predecir el valor de una variable, conocido el valor
de la otra, por ejemplo, tecleando: =TENDENCIA (B2:B6, A2:A6, 5)
obtenemos el peso esperado para una edad de cinco años. La otra función nos mide el error estimado de una variable al ser estimado su valor por la recta de regresión. Su forma es: =ERROR.TÍPICO.XY. (B2:B6, A2:A6), devuelve el error típico del valor de Y previsto para cada X.
obtenemos el peso esperado para una edad de cinco años. La otra función nos mide el error estimado de una variable al ser estimado su valor por la recta de regresión. Su forma es: =ERROR.TÍPICO.XY. (B2:B6, A2:A6), devuelve el error típico del valor de Y previsto para cada X.
También podemos hacer
la nube de puntos. Marcando los datos introducidos, pulsamos el
botón de gráficos, seleccionamos diagrama de dispersión y a través de las
ventanas de diálogos damos nombre a los ejes, hacemos la división en los
mismos.
sábado, 2 de febrero de 2013
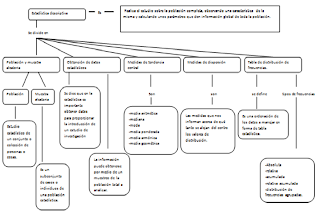
Estadistica descriptiva
1.1 “ POBLACIÓN Y MUESTRA ALEATORIA”
-Población
Todo
estudio estadístico ha de estar referido a un conjunto o colección de personas
o cosas lo que se denomina como población.
Las
personas o cosas que forman parte de la población se denominan elementos. En
sentido estadístico un elemento puede ser algo con existencia real, como un
automóvil o una casa, o algo más abstracto como la temperatura, un voto, o un
intervalo de tiempo.
A su
vez, cada elemento de la población tiene una serie de características que
pueden ser objeto del estudio estadístico.
Luego
por tanto de cada elemento de la población podremos estudiar uno o más aspectos
cualidades o caracteres que se llaman variables estadísticas.
La
población puede ser según su tamaño de dos tipos:
Población finita: el número de elementos que la forman es finito, por ejemplo el número
de alumnos de un centro de enseñanza.
Población infinita: el número de elementos que la forman es infinito, o tan grande que
pudiesen considerarse infinitos. Como por ejemplo si se realizase un estudio
sobre los productos que hay en el mercado.
Ahora
bien, normalmente en un estudio estadístico, no se puede trabajar con todos los
elementos de la población sino que se realiza sobre un subconjunto de la misma
al que se le llama muestra, es decir un
determinado número de elementos de la población.
-Muestra Aleatoria
Una muestra estadística o muestra aleatoria o simplemente muestra es un subconjunto de
casos o individuos de una población estadística.
Las muestras se
obtienen con la intención de inferir propiedades de la totalidad de la
población, para lo cual deben ser representativas de la misma. Para cumplir
esta característica la inclusión de sujetos en la muestra debe seguir una técnica de muestreo.
Por otra parte, en
ocasiones, el muestreo puede ser más exacto que el estudio de toda la población
porque el manejo de un menor número de datos provoca también menos errores en
su manipulación.
El número de sujetos que
componen la muestra suele ser inferior que el de la población, pero suficiente
para que la estimación de los parámetros determinados tenga un nivel de confianza adecuado. Para que el tamaño de la muestra sea idóneo es preciso recurrir a su
cálculo.
Espacio Muestral
El espacio muestral del que se toma
una muestra concreta está formado por el conjunto de todas las posibles
muestras que se pueden extraer de una población mediante una determinada técnica de muestreo.
Parámetro o Estadístico muestral
Un parámetro
estadístico o simplemente un estadístico muestral es cualquier valor calculado a partir de la
muestra, como por ejemplo la media, varianza o una proporción, que describe a una
población y puede ser estimado a partir de una muestra. Valor de la población.
Estimación
Una estimación es cualquier
técnica para conocer un valor aproximado de un parámetro referido a la
población, a partir de los estadísticos muestrales calculados a partir de los
elementos de la muestra.
Nivel de confianza
El nivel de confianza de una aseveración basada en la inferencia estadística es una medida de la bondad de la
estimación realizada a partir de estadísticos muestrales.
Ejemplo
La descripción de una
muestra, y los resultados obtenidos sobre ella, puede ser del tipo mostrado en
el siguiente ejemplo:
Dimensión
de la población: ej. 222.222 habitantes
Probabilidad del evento: ej. Hombre o Mujer 50%
Nivel de
confianza: ej. 96%
Desviación
tolerada: ej. 5% Resultado ej. 196
Tamaño de
la muestra: ej. 270
La interpretación de
esos datos sería la siguiente:
·
La población a investigar tiene 222.222
habitantes y queremos saber cuántos son hombres o mujeres.
·
Estimamos en un 50% para cada sexo y para el
propósito del estudio es suficiente un 90% de seguridad con un nivel entre 90 -
5 y 90 + 5.
·
Generamos una tabla de 270 números al azar entre
1 y 222.222 y en un censo numerado comprobamos el género para los
seleccionados.
Ventajas de la elección de una
muestra
El estudio de muestras
es preferible, en la mayoría de los casos, por las siguientes razones:
1. Si la población es muy
grande (en ocasiones, infinita, como ocurre en determinados experimentos aleatorios) y, por tanto, imposible de analizar en su
totalidad.
2. Las características de
la población varían si el estudio se prolonga demasiado tiempo.
3. Reducción de
costos: al estudiar una pequeña parte de la población, los gastos de
recogida y tratamiento de los datos serán menores que si los obtenemos del
total de la población.
4. Rapidez: al
reducir el tiempo de recogida y tratamiento de los datos, se consigue mayor
rapidez.
5. Viabilidad: la
elección de una muestra permite la realización de estudios que serían imposible
hacerlo sobre el total de la población.
6. La población es
suficientemente homogénea respecto a la característica medida, con lo cual
resultaría inútil malgastar recursos en un análisis exhaustivo (por ejemplo,
muestras sanguíneas).
7. El proceso de estudio
es destructivo o es necesario consumir un artículo para extraer la muestra
(ejemplos: vida media de una bombilla, carga soportada por una cuerda,
precisión de un proyectil, etc.).
Descripción matemática de una muestra
aleatoria
El uso de muestras
para deducir fiablemente características de la población requiere que se trate
con muestras aleatorias. Si la muestra estadística considerada no
constituye una muestra aleatoria las conclusiones basadas en dicha muestra no
son fiables y en general estarán sesgadas en algún aspecto.
En términos
matemáticos, dada una variable aleatoria X con una distribución de probabilidad F, una muestra aleatoria de
tamaño N es un conjunto finito de N variables independientes, con la misma distribución de
probabilidad F.1
En general, resulta
muy difícil comprobar si una determinada muestra es o no aleatoria, cosa que
sólo puede hacerse considerando otro tipo de muestreos aleatorios robustos que
permitan decir si la primera muestra era aleatoria o no.
1.2 “Obtención de datos
estadísticos”
¿Para qué necesitamos obtener datos en estadística?
En la estadística es importante obtener datos, para
Proporcionar la introducción imprescindible para un estudio de investigación,
Medir el desempeño en un servicio o proceso de producción, Nos Ayudar en la
formulación de alternativas para la toma
de decisiones. Algunos ejemplos de para qué es necesario obtener datos son los
siguientes:
n Un
gerente desea investigar si la calidad del servicio o de los productos se
ajustan a los estándares de la compañía.
¿De qué manera podemos obtener datos
estadísticos?
La información puede obtenerse por muestreo, observando
pasivamente una muestra y anotando los valores de las variables, o por diseño
de experimentos, fijando los valores en ciertas variables y observando la
respuesta de otras.
El muestreo es por lo tanto
una herramienta de la investigación científica, cuya función Básica es
determinar que parte de una
población debe examinarse, con la finalidad de hacer Inferencias sobre
dicha población. Para que una muestra sea representativa, y por lo tanto útil, debe
de reflejar las similitudes y diferencias encontradas en la población, es decir
ejemplificar las características de ésta.
Tipos de muestreo
Existen diferentes criterios de clasificación de los
diferentes tipos de muestreo, aunque en general pueden dividirse en dos grandes
grupos: métodos de muestreo probabilísticos y métodos de muestreo no probabilísticos.
1. Muestreo probabilístico
Los métodos de muestreo probabilísticos son aquellos que se
basan en el principio de equiprobabilidad. Es decir, aquellos en los que todos
los individuos tienen la misma probabilidad de Ser elegidos para formar parte
de una muestra y, consiguientemente, todas las posibles muestras
Dentro de los métodos de muestreo probabilísticos encontramos
los siguientes tipos:
1.1. Muestreo aleatorio
simple:
El procedimiento empleado es el siguiente:
1) se asigna un número a cada individuo de la población.
2) A través de algún medio mecánico (bolas dentro de una
bolsa, tablas de números aleatorios, números aleatorios generados con una
calculadora u ordenador, etc.) se eligen tantos sujetos como sea necesario para
completar el tamaño de muestra requerido.
1.2. Muestreo aleatorio
sistemático:
Este procedimiento exige, como el anterior, numerar todos los
elementos de la población,
Pero en lugar de extraer números aleatorios sólo se extrae
uno. Se parte de ese número aleatorio “i”, que es un número elegido al azar, y
los elementos que integran la muestra son los que ocupa los lugares i, i+k,
i+2k, i+3k,...,i+(n-1)k, es decir se toman los individuos de k en k, siendo k
el resultado de dividir el tamaño de la población entre el tamaño de la muestra:
k= N/n. El número i que empleamos como punto de partida será un número al azar
entre 1 y k.
1.3. Muestreo aleatorio
estratificado:
Trata de evitar las dificultades que presentan los anteriores
ya que simplifican los procesos y suelen reducir el error maestral para un
tamaño dado de la muestra. Consiste en considerar categorías típicas diferentes
entre sí (estratos) que poseen gran homogeneidad respecto a alguna característica
(se puede estratificar, por ejemplo, según la profesión, el municipio de
residencia, el sexo, el estado civil, etc.). Lo que se pretende con este tipo
de muestreo es asegurarse de que todos los estratos de interés estarán
representados adecuadamente en la muestra. Cada estrato funciona
independientemente, pudiendo aplicarse dentro de ellos el muestreo aleatorio
simple o el estratificado para elegir los elementos concretos que formarán parte
de la muestra. En ocasiones las dificultades que plantean son demasiado
grandes, pues exige un conocimiento detallado de la población. (Tamaño
geográfico, sexos, edades,...)
1.4. Muestreo aleatorio
por conglomerados:
Los métodos presentados hasta ahora están pensados para
seleccionar directamente los elementos de la población, es decir, que las
unidades muéstrales son los elementos de la población.
2. Métodos de muestreo no probabilísticos
A veces, para estudios exploratorios, el muestreo probabilístico
resulta excesivamente costoso y se acude a métodos no probabilísticos, aun
siendo conscientes de que no sirven para realizar generalizaciones
(estimaciones inferenciales sobre la población), pues no se tiene certeza de
que la muestra extraída sea representativa, ya que no todos los sujetos de la
población tienen la misma probabilidad de ser elegidos. En general se seleccionan
a los sujetos siguiendo determinados criterios procurando, en la medida de lo
posible, que la muestra sea representativa.
2.1. Muestreo por
cuotas:
También denominado en ocasiones "accidental". Se
asienta generalmente sobre la base de un buen conocimiento de los estratos de
la población y/o de los individuos más "representativos" o
"adecuados" para los fines de la investigación. Mantiene, por tanto,
semejanzas con el muestreo aleatorio estratificado, pero no tiene el carácter
de aleatoriedad de aquél.
2.2. Muestreo
intencional o de conveniencia:
Este tipo de muestreo se caracteriza por un esfuerzo deliberado
de obtener muestras "representativas" mediante la inclusión en la
muestra de grupos supuestamente típicos. Es muy frecuente su utilización en
sondeos preelectorales de zonas que en anteriores votaciones han marcado
tendencias de voto.
2.3. Bola de nieve:
Se localiza a algunos individuos, los cuales conducen a otros,
y estos a otros, y así hasta conseguir una muestra suficiente. Este tipo se
emplea muy frecuentemente cuando se hacen estudios con poblaciones
"marginales", delincuentes, sectas, determinados tipos de enfermos,
etc.
2.4. Muestreo
Discrecional:
A criterio del investigador los elementos son elegidos sobre
lo que él cree que pueden aportar al estudio.
1.3 “Medidas de tendencia central”
Al
describir grupos de observaciones, con frecuencia es conveniente resumir la
información con un solo número. Este número que, para tal fin, suele situarse
hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización.
Entre las medidas de tendencia
central tenemos:
·
Media aritmética.
Media aritmética o Media
Es el promedio de un conjunto de
valores.
Ejemplo, la media aritmética de 34, 27,
45, 55, 22, 34 (seis valores) es Se
obtiene de la suma de todos los valores dividida entre la cantidad de valores.
Media Ponderada
Es apropiada cuando en un conjunto de datos cada uno de ellos tiene una importancia relativa (o peso) respecto de los demás datos
Se obtiene del cociente entre la suma de los
productos de cada dato por su peso o ponderación y la suma de los pesos.
Media geométrica
Es un
promedio muy útil en conjuntos de números que son interpretados en orden de su
producto, no de su suma.
Se obtiene de la multiplicación de
todos los valores, elevada a la potencia de la cantidad de valores dividiendo a
uno ‘‘1’.
Media armónica
La media armónica es un promedio muy útil en
conjuntos de números que se definen en relación con alguna unidad.
Mediana
Representa el valor de la variable de posición
central en un conjunto de datos ordenados.
Ejemplo:
tenemos el siguiente conjunto de números 8,3,7,4,11,2,9,4,10,11,4 ordenamos:
2,3,4,4,4,7,8,9,10,11,11 En esta secuencia la mediana es 7, que es el número
central. Y si tuviésemos: 8,3,7,4,11,9,4,10,11,4, entonces ordenamos:
3,4,4,4,7,8,9,10,11,11 y la mediana (Md) está en: los números centrales son 7 y
8, lo que haces es sumar 7 + 8 y divides entre 2 y Md= 7.5.
Los
pasos son:
1. Ordena
los valores en orden del menor al mayor.
2. Cuenta
de derecha a izquierda, o al revés, hasta encontrar el valor o valores medios.
Moda
Es el valor con una mayor frecuencia en una
distribución de datos.
Ejemplo Encontrar la estatura modal de un grupo que se encuentra
distribuido de la siguiente forma:
Entre 1,1 y 1,15 hay 1 estudiante
Entre
1,2 y 1,25 hay 2 estudiantes
Entre
1,3 y 1,35 hay 2 estudiantes
Entre
1,45 y 1,55 hay 3 estudiantes
Entre
1,5 y 1,6 hay 4 estudiantes
Entre
1,6 y 1,7 hay 10 estudiantes
Entre
1,7 y 1,8 hay 8 estudiantes
Entre
1,8 y 1,9 hay 2 estudiantes
Clase modal = 1,6 y 1,7 (es la que tiene frecuencia absoluta más alta: 10).
1.4 “Medidas de dispersión”
Las medidas de dispersión nos informan sobre
cuánto se alejan del centro los valores de la distribución.
Las medidas de dispersión son:
Rango o
recorrido
El rango es la diferencia entre el mayor y el menor
de los datos de una distribución estadística.
Desviación
media
La desviación respecto a la media es la diferencia
entre cada valor de la variable estadística y la media aritmética.
Di = x - x
La desviación media es la media aritmética de los
valores absolutos de las desviaciones respecto a la
media.
Ejemplo
Calcular la desviación media de la
distribución:
9, 3, 8, 8, 9, 8, 9, 18
Desviación media para datos
agrupados
Si los datos vienen agrupados en una tabla de
frecuencias, la expresión de la desviación media es:
Varianza
La varianza es la media aritmética del cuadrado de
las desviaciones respecto a la media de una distribución estadística.
Propiedades de la varianza
ü La varianza será siempre un valor
positivo o cero, en el caso de que las puntuaciones sean iguales.
ü Si a todos los valores de la variable
se les suma un número la varianza no varía.
ü Si todos los valores de la variable se
multiplican por un número la varianza queda multiplicada por el cuadrado de
dicho número.
ü Si tenemos varias distribuciones con la misma
media y conocemos sus respectivas varianzas se puede calcular la varianza
total.
1.5 “Tabla de distribución de
frecuencias”
La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente
Tipos de frecuencias:
Frecuencia absoluta
La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.
Se representa por fi.
Frecuencia relativa
La frecuencia
relativa es el cociente entre
la frecuencia
absoluta de un
determinado valor y el número total de
datos. Se puede expresar en tantos por ciento y se representa
por ni.
Frecuencia acumulada
La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado. Se representa por Fi.
La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado. Se representa por Fi.
Frecuencia relativa acumulada
La frecuencia relativa acumulada es el cociente entre
la frecuencia acumulada de un
determinado valor y el número total de datos. Se
puede expresar en tantos por ciento.
Distribución de
frecuencias agrupadas
La distribución
de frecuencias agrupadas o tabla
con datos agrupados se emplea si las variables toman un número
grande de valores o la variable
es continua.
Suscribirse a:
Comentarios (Atom)





.png)